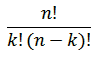ترکیب ریاضی

ترکیب

به طور کلی ترکیب های k تایی از n شی متمایز به انتخاب های k تایی از n شیء اطلاق می شود که در آن ها ترتیب فاقد اهمیت است.

تعداد ترکیب های k تایی از n شئ متمایز از فرمول زیر محاسبه می شود.

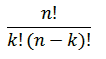
در ضمن این تعداد را با نماد های زیر نیز نشان می دهند.

 

این نکته نیز قابل توجه است که همیشه n بزرگ تر یا مساوی k می باشد .

 مثال: بر روی محیط یک دایره هفت نقطه قرار گرفته است ، از اتصال این نقاط چند مثلث می توان رسم کرد.
چون هر مثلث از اتصال سه نقطه ایجاد می شود ، بنابراین:

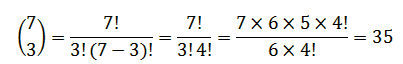
بنابراین 35 مثلث می توان رسم کرد.

 

مثال: حاصل عبارات زیر را به دست آورید.

 
 

---

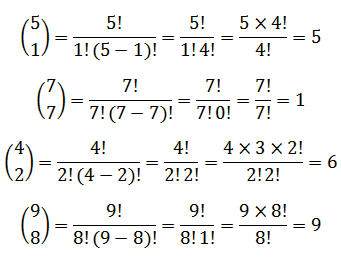
محاسبه ترکیب k شی از n شی با استفاده از Dynamic Programming قسمت اول

شاید بدونید که در مباحث ریاضی مبحثی نه چندان ساده ولی شیرین به نام
آنالیز ترکیبی داریم که بیشتر کارش اینه که حالت های مختلف یک اتفاق رو
بشماره. ساده ترین حالتش یه تاس رو پرتاب کنیم هوا چند حالت امکان داره روی
زمین قرار بگیره؟! مسلما شش تا . حالا اگه دوتا تاس رو انداختیم بالا چند
حالت ؟!‌ طبق اصل ضرب ۳۶ حالت خواهیم داشت. ( اصلا قصد صحبت در مورد اینا
رو ندارم)

خب بذارید یه حالت دیگه رو بررسی کنیم. اگه شما بخواهید از یه سری شی
متمایز ( مثلا یه سری آدم) که تعدادشون n تا است k  نفر رو برای کوه نوردی
انتخاب کنید چند حالت امکان داره؟ مثلا مدیر یه مدرسه به چند حالت میتونه
از بین ۲۰ نفر از دانش آموزای یک کلاس ۴ نفر رو برای نظافت دستشویی های
مدرسه انتخاب کنه؟خخخ

وقتی صحبت از انتخاب k نفر از n نفر میشه و ترتیب انتخاب ها مهم نیست
(الان میگم یعنی چی مهم نیست ) باید از فرمول ترکیب استفاده کنیم که با
نماد C(n,k) مشخص میشه. و مقدارش برابر هست با  : ( تصویر از ویکی پدیا)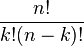

اما اینکه گفتم ترتیب انتخاب مهم نیست یعنی چی ؟‌ ببینید اگه همون مدیر
بخواد از ۲۰ نفر ۳ نفر رو به عنوان رتبه ۱و۲و۳ کلاس انتخاب کنه اینکه آقای
سعید دادخواه به عنوان رتبه یک انتخاب بشه و یا رتبه دو ویا سه باهم متفاوت
هستش ولی وقتی برای تمیز کردن دستشویی انتخاب میشد مهم نبود نفر اول بود
که انتخاب میشد یا نفر دوم یا … پس منظور از اهمیت ترتیب انتخاب اینه.

خب حالا میخوایم یه تابع به نام comb بنویسیم که دوتا int n , int k
 دریافت کنه مقدار بالا رو محاسبه کنه. چه راهی به ذهنتون میرسه؟ اول بیایم
فاکتوریل n رو حساب کنیم بعد تقسیم بر مخرجش کنیم؟ راه خوبیه ولی راه زیبا
تری میخوایم

استفاده از شیوه تفرقه بینداز و حکومت کن

یکی از شیوه های طراحی الگوریتم شیوه Divide And Conquer هستش یعنی
تفرقه بینداز و حکومت کن. فکر کنم تاریخچه اش هم مربوط به انگلیسی هاست که
منطقشون اینه که برای حکومت بر مردمی باید بینشون تفرقه انداخت.

ولی این شیوه چطوریه؟ میگه که وقتی میتونی سوالی رو بشکنی به دو یا چند
سوال کوچکتر این کار رو بکن و سوال های کوچکتر رو حل کن و بعد سوال اصلی رو
حل کن. مثلا فرض کنید میخوایم آرایه ای از اعداد رو که به صورت زیر هستش
مرتب کنیم:

۵

۴

۴۴

۶

۹۰

۱۲

۲

۱۲

طبق این روش میتونیم اول چهار تا سلول سمت چپ رو مرتب کنیم بعد چهار تا
سلول راست رو بعد هم کل کار رو. برای مرتب کردن چهارتای سمت چپ بازم
میتونیم مساله رو بشکنیم و دوتای سمت چپ رو اول مرتب کنیم بعد سمت راست و
بعد کل اونا رو. به تصویر زیر که بازم از ویکی پدیا گرفته شده دقت کنید تا متوجه منظورم بشید.

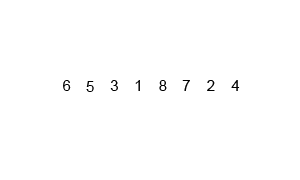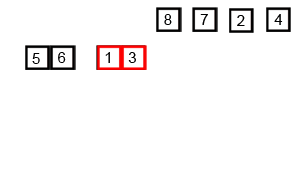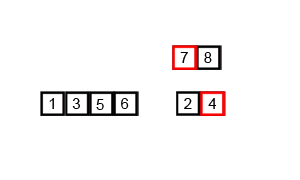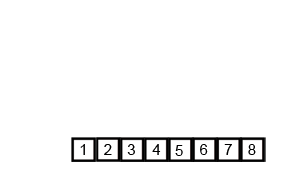خب آیا میشه از شیوه تقسم و غلبه (همین که الان گفتیم )‌برای محاسبه ترکیب k از n استفاده کرد. بعله میشه. به فرمول زیر دقت کنید:

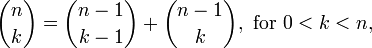خیلی
عالیه ! ما تونستیم ترکیب k از n رو به دو قسمت تقسیم کنیم. برای درک این
فرمول این اثبات شهودی رو بخونید :‌ وقتی میخوایم از بین ۲۰ دانش آموز ۴ تا
واسه تمیز کردن دشویی انتخاب کنیم مث این میمونه که این حالت رو در نظر
بگیریم که سعید دادخواه رو از قبل انتخاب کردیم ( قسمت اول فرمول) و از
بقیه ۱۹ نفر سه نفر رو انتخاب می کنیم ( ترکیب k-1 از n-1 ) یا این حالت که
اصن بی خیال سعید دادخواه شدیم و از ۱۹ نفر دیگه ۴ نفر رو انتخاب کنیم (
قسمت دوم ترکیب k از n-1 )

خب پس با این فرمول میتونیم مقدار ترکیب k از n  رو حساب کنیم. با این
فرض که میدونیم که ترکیب n از n ( یعنی انتخاب n نفر از n نفر)‌میشه یک (
فقط یک حالت امکان داره از n نفر n نفر رو انتخاب کرد ) و ترکیب ۰ نفر از n
نفر هم میشه یک بازم. با این تفاسیر میشه تابع زیر رو برای محاسبه ترکیب k
از n نوشت.

#include <iostream>

using namespace std;
int comb(int n, int k)
{
if(n==k||k==0)
return 1;
return comb(n-1,k-1)+comb(n-1,k);
}

int main()
{
cout<< comb(8,3);
return 0;
}

123456789101112131415

#include <iostream> usingnamespacestd;intcomb(intn,intk){    if(n==k||k==0)        return1;    returncomb(n–1,k–1)+comb(n–1,k);} intmain(){    cout<<comb(8,3);    return0;}

خب حالا Dynamic Programming چی میگه این وسط. واقع قضیه اینه که استفاده
از شیوه Divide and Conquer برای این مساله Order زمانی مناسبی نداره (
یعنی خیلی الکی طول می کشه) باید دقت کرد که شیوه تقسیم و غلبه (همون
divide and conquer) فقط برای مسایلی مناسب است که سایز  مسایل کوچکتری که
در اثر تقسیم بدست میاد خیلی کوچکتر از سایز مساله اصلی باشه در حالی که
اینجا اینطور نیست . مساله اصلی ترکیب k از n هستش در حالی که ریز مساله
ترکیب k-1 از n-1 . نکته دوم اینه که شیوه تقسیم و غلبه جایی بدرد میخوره
که مسایل ریز ( که در اثر تقسیم به دست آمده اند) با هم همپوشانی نداشته
باشند. یعنی ممکنه یه جایی از ریز مساله ها یه مقداری رو حساب کنیم که قبلا
هم حساب شده. مرض که نداریم هی حساب کنیم.

---