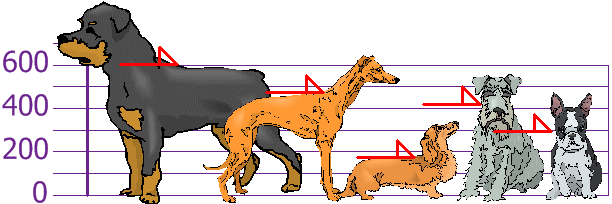
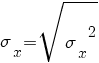مفهوم واریانس و انحراف معیار

درک واریانس (variance) و انحراف معیار(Standard Deviation)

انحراف معیار استاندارد یا واریانس یعنی این که چقدر از حد نرمال(میانگین) فاصله داریم؟

معنی انحراف معیار استاندارد

انحراف معیار استاندارد ابزار سنجش مقدار پراکندگی داده هاست و با نماد
یونانی σ در زمانی که داده ها از شامل کل جامعه است و نماد s زمانی که
داده ها دسته ای از جامعه را شامل می شود نمایش داده می شود.فرمول محاسبه
این ابزار به این گونه تعریف میشود:

رادیکال واریانس برابر است با انحراف معیار.

$sigma_x=sqrt{{sigma_x}^2}$

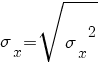
با استفاده از انحراف معیار
استاندار می توانیم استانداردی داشته باشیم تا تشخیص دهیم چه چیزی نرمال
است، چه چیزی بیشتر یا کمتر از نرمال است.

واریانس چیست؟

برابر است با داده ها منهای میانگین کل داده ها به توان دو

1-زمانی که کل جامعه در شمارش موجود است

${sigma_x}^2=(x_i-mu_x)^2/N$

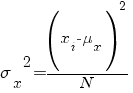
2-زمانی که فقط دسته ای از اطلاعات موجود است

${s_x}^2=(x_i-overline{x})^2/{N-1}$

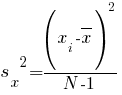
چرا در بررسی کل جامع N را در مخرج کسر و در بررسی بخشی از جامع مقدار N-1 را قرار می دهیم؟[2]

پاسخ: زمانی که شما از یک نمونه ی N تایی صحبت به میان می آورید پس
میانگین حقیقی نخواهد بود، بلکه تخمینی از میانگین واقعی جامعه است فلذا یک
درجه ی آزادی از آن کسر می گردد.

مثالی برای درک کامل مبحث واریانس[1]

در شکل زیر نمونه ای 5 تایی از سگ ها را برای ارزیابی قد آنها داریم:

ارتفاع سگها از شانه برابر است با 600 ،470،170،430،300 میلی متر

حال به یافتن میانگین، واریانس و انحراف معیار استاندارد می پردازیم.

مرحله ی اول یافتن میانگین است و به صورت زیر محاسبه می شود

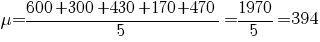
بنابراین میانگین یا متوسط قد برابر 394 میلی متر است ، در شکل زیر میانگین با خط سبز نمایش داده شده است

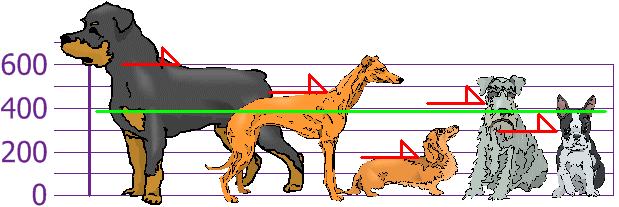حالا ما می توانیم به بررسی تفاوت قد هر کدام از سگها به نسبت خط میانگین بپردازیم، این امر در عکس زیر به خوبی نمایش داده شده است.

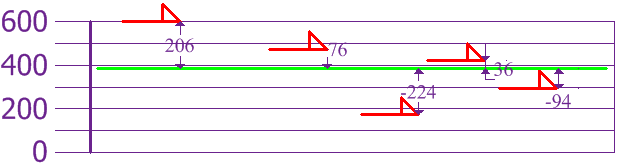برای محاسبه واریانس به صورت زیر عمل می کنیم

$sigma^2={{{206^2}+{76^2}+{36^2}+{-224^2}+{-94^2}}/5}=21,704$

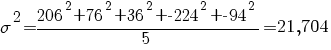
برای محاسبه انحراف معیار استاندارد به صورت زیر عمل می کنیم

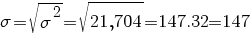$sigma=sqrt{sigma^2}=sqrt{21,704}=147.32= 147$ (نزدیک ترین عدد به میلی متر)

با توجه به انحراف معیار استاندارد( 147 میلی متر)می توانیم بگویم که
سگی با قد 600 بسیار قد بلندتر از استاندارد و سگی با قد 170 بسیار کوچکتر
از حد استاندارد است.

نکته ی قابل توجه اینکه در این مثال چون کل جامعه ی آماری ما شامل 5 سگ
بود و ما همه ی آنها را لحاظ کرده ایم پس از نماد σ استفاده کرده و در مخرج
کسر از N استفاده کردیم ، حال اگر در مثال گفته می شد که این 5 سگ به صورت
نمونه انتخاب شده اند در این صورت باید نماد به s تغییر کرده و در مخرج
کسر نیز از N-1 استفاده می کردیم.

نکته:

در نرم افزار اکسل چندین فرمول برای محاسبه واریانس وجود دارد که در اینجا دو مورد از آنها را معرفی می کنیم:

var.p:واریانس یک جامعه را محاسبه می کند، مانند مثال بالا.
var.s: واریانس نمونه را محاسبه می کند،در حقیقت در مخرج کسر n-1 می گذارد.

شاخص های پراكندگي

مبنای علم پراکندگی یا همان تغییر است و در
صورتی که تغییر وجود نداشته باشد، علم نیز بی معناست. علم به دنبال تبیین
این پراکندگی ها و تغیرات است.

اندازه هاي مركزي مانند ميانگين،
ميانه و نما توصيف كننده وضعيت كامل توزيع داده ها نيستند. به عبارت ديگر
دو مجموعه داده كه داراي ميانگين هاي يكسان هستند ممكن است پراكندگي
متفاوتي داشته باشند و زماني مي‌توان توزيع داده‌ها را دقيقاً توصيف نمود
كه علاوه بر شناخت معيار مناسبي براي مركزيت آن، معياري را هم براي
پراكندگي آنها تعيين نمود .کاربرد شاخص های پراکندگی تنها برای داده های
فاصله ای و نسبتی است. مهمترین آنها عبارتند از:

دامنه تغییرات، واریانس، انحراف معیار، انحراف چارکی، انحراف متوسط،

دامنه تغییرات به شکل روبرو محاسبه می شود. R= Xn-X1

كه Xn بزرگترين اندازه و X1 كوچكترين اندازه مشاهده شده است.

دامنه
نيز همانند ميانگين تحت تأثير داده هاي پرت قرار مي گيرد و در چنين حالاتي
يك معيار مناسب پراكندگي نيست. به علاوه، چون براي محاسبه دامنه فقط از دو
اندازه بزرگترين مشاهده و كوچكترين مشاهده استفاده مي شود معمولاً معيار
رضايت بخشي براي پراكندگي به حساب نمي آيد.

واریانس و انحراف معیار

مفديدترين
اندازه پراكندگي واريانس و يا جذر آن، انحراف معيار داده ها است. اندازه
انحراف معيار به ما مي گويد كه مشاهدات تا چه مقدار در اطراف ميانگين آنها
قرار دارند، يك اندازه كم براي انحرف معيار مجموعه اي از داده ها نشان
دهنده اين واقعيت است كه داده ها در دامنه كوچكي حول ميانگين پراكنده
شده‌اند و بالعكس انحراف معيار بزرگ بيان كننده دامنه گسترده‌تري است كه
داده ها در حول ميانگين پراكنده گرديده اند. انحراف معیار ریشه دوم مثبت
واریانس است که برای جامعه آن را با و برای نمونه آن را با s نشان می
دهیم. نحوه محاسبه واریانس به این شکل است که جذر آن انحراف معیار را به ما
می دهد.

اگر واريانس را از جدول توزيع فراواني به دست آوريم خواهيم داشت:

اگر همه ي داده هاي آماري با هم برابر باشند، واريانس و انحراف معيار برابر صفر خواهد بود.

دلیل استفاده از انحراف استاندارد این است که مقیاس2 S با مقیاس نمرات یکی نیست و راه حل استفاده از Sاست.

انحراف
استاندارد یکی از مهم ترین شاخصه های هر توزیع آماری است و در توزیع های
مختلف به روش های مختلف محاسبه می شود. ممکن است این سوال پرسیده شود که
داده های تجربی انطباق دقیق با توزیع های نظری آماری ندارد. برای تعیین
شاخص های پراکندگی این توزیعات پژوهشگران چه می کنند؟ این موضوع یکی از
دغدغه های پژوهشگران آماری است که از روش های پیچیده ای به محاسبه انحراف
استاندارد می پردازند.

انحراف متوسط: (که به آن میانگین قدر
مطلق انحراف ها هم می گویند)، فاصله داده Xi از میانگین را انحراف از
میانگین Xi گویند که به صورت محاسبه می شود. اگر این مقدار را برای
تمامی داده ها محاسبه کنیم و از نتیجه میانگین بگیریم، میانگین انحرافات
بدست خواهد آمد که عبارت است از:

از
آنجا که میانگین انحرافات به تمام داده ها وابسته است معیار مناسبی برای
سنجش پراکندگی داده ها محسوب می شود اما به دلیل وجود قدر مطلق در فرمول،
محاسبه آن مشکل است و نمی توان آن را ساده نمود، بنابراین واریانس و انحراف
استاندارد شاخص های مناسب تری هستند.

انحراف چارکی

انحراف چارکی عبارت است از: نصف فاصله بین چارکهای اول و سوم و از طریق فرمول زیر بدست می آید:

ابتدا اعداد را از کوچک به بزرگ مرتب می کنیم.

محاسبه میانه یا چارک دوم اعداد

محاسبه میانه اعداد سمت چپ

محاسبه میانه اعداد سمت راست

ویژگیهای انحراف چارک:

انحراف
چارکی خیلی کم تحت تأثیر اختلافهای تصادفی بین نمونه های انتخاب شده قرار
می گیرد چون همانند میانه تحت تأثیر نمره های خیلی بزرگ یا خیلی کوچک قرار
نمی گیرد. شرایط استفاده آن همانند میانه است و هر دو یک خانوادة آماری را
تشکیل می دهند. در زمانی مورد استفاده قرار می گیرند که مقیاس حداقل فاصله
ای باشد.

توزیع نرمال و شکل آن

توزیع نرمال یکی از توزیع‌های
احتمالاتی پیوستهٔ مهم است. توزیع نرمال استاندارد توزیعی با میانگین صفرو
انحراف استاندارد واحد است. به علت شباهت این شکل به زنگوله به آن انحنای
زنگوله‌ای نیز گفته می‌شود.

دلیل اهمیت توزیع نرمال از وجود قضیه حد
مرکزی ناشی می‌شود. این قضیه می‌گوید هنگامی که تعداد بسیار زیادی متغیر
تصادفی با توزیع دل‌خواه و با واریانس محدود را با هم جمع کنیم و میانگین
بگیریم، توزیع نهایی به توزیع نرمال میل می‌کند. به همین خاطر

هنگامی که شاهد تأثیر جمعی‌ بسیاری از پدیده‌های تصادفی هستیم، نتیجهٔ نهایی با توزیع نرمال قابل توصیف است.

این
منحنی دارای خواص بسیار جالبی است از آن جمله که نسبت به محور عمودی
متقارن می باشد، نیمی از مساحت زیر منحنی بالای مقدار متوسط و نیمه دیگر در
پایین مقدار متوسط قرار دارد و اینکه هرچه از طرفین به مرکز مختصات نزدیک
می شویم، ارتفاع منحنی بیشتر می شود.

شاخص های نماینده توزیع نرمال:

میانگین (µ): نشان دهنده تراکم داده ها حول یک مقدار

انحراف معیار (σ): نشان دهنده میزان پراکندگی داده ها از میانگین

مثال کاربرد µ و σ:

با
رسم نمودار فراوانی داده های پیوسته عموما یکی از اشکال زیر بدست می آید؛
که چگونگی قرار گرفتن میانگین و میانه ومد را در اشکال زیر مشاهده می شود.

کجی به 2 دلیل ایجاد می شود:

متغیر
ماهیتا کجی دارد: مثل بزهکاری که در این موارد باید از آزمون های
ناپارامتری استفاده کنیم مثلا به جای مقایسه میانگین ها از میانه استفاده
می کنیم.

داده های پرت باعث کجی شده اند.

راه حل این مشکل این 3 راهکار است: حذف(برای مقادیر پرت)، وینزوری کردن (آرایش کردن)، Trimned (پیرایش کردن)

در
تحلیل داده ها اولین قدم تمییز کردن داده هاست. روش هایی که برای برخورد
با داده های گمشده وجود دارد می تواند برای برخورد با داده های پرت نیز
استفاده شود. این روش ها گستره ای از حذف تا شبیه سازی کردن داده ها را در
بر می گیرد. نرم افزار SPSS ورژن 19 که متعلق به شرکت آی بی ام است، فرمان
های اشاره شده را داراست.

ضریب کشیدگی: نشان دهنده میزان کشیدگی منحنی می باشد و به صورت زیر تعریف می شود:

دو منحنی زیر متقارن می باشند اما ضریب کشیدگی در آنها متفاوت است:

یکی
از کاربرد های مهم منحنی نرمال سطوح زیر منحنی آن می باشد. کاربرد این
سطوح را می توان در تعیین فاصله ی اطمینان و همچنین تعیین نقاط برش برای
متغیرهای دارای توزیع نرمال مشاهده کرد.

سطح زیر منحنی نرمال برای مقادیر متفاوت  و 

یکی
دیگر از مهمترین منحنی های وابسته به منحنی نرمال منحنی اجایو نرمال یا
همان منحنی تراکمی نرمال است. این منحنی یکی از پرکاربرد ترین منحنی ها در
علوم مختلف و مخصوصا علوم انسانی است. این منحنی در روانسنجی و مخصوصا
نظریه ی جدید روانسنجی یعنی نظریه ی سوال پاسخ استفاده می شود. با توجه به
اینگه بسیاری از فرایندهای موجود در طبیعت و در علوم مختلف مانند مدیریت,
کنترل پروژه از این منحنی پیروی می کنند در برآورد پارامترهای مختلف یا
برنامه ریزی به فراوانی مورد استفاده قرار می گیرد. یکی از کاربردهای مهم
این منحنی در روانشناسی بالینی استفاده از آن برای پیدا کردن الگوهای رشد
است. از آنجا که رشد دارای الگویی مانند منحنی نرمال تراکمی است می توان از
آن در روانشناسی رشد و یا در شبیه سازی ها استفاده نمود. کاربرد این منحنی
را می توان در آی تی و در هوش مصنوعی و داده کاوی مشاهده کرد. در زیر شکلی
از این منحنی ارائه شده است.

از آنجا که تابع
اجایو نرمال شناخته شده است و همچنین به دلیل شباهتی که بین این تابع با
تابع لجستیک دارد با اضافه کردن مقدار ثابت در فرمول های مربوط به تابع
لجستک آنها را به تابع نرمال تراکمی تبدیل می کنند. بنابراین کارکردهای
زیادی که برای تابع لجستیک متصور است برای تابع اجایو نرمال نیز قابل تصور
خواهد بود.

بسیاری از توابع دیگر مانند دوجمله به تابع نرمال تقریب
زده می شوند و در ضمن بسیاری از توابع قابل تبدیل به تابع نرمال اند مانند
تابع فیشر یا همان تابع معروف F و یا تابع خی دو.

گاهی در مطالعاتی
که انجام می شود، نیاز است علاوه بر اینکه تک تک متغیرها نرمال باشند،
ترکیب آنها نیز نرمال باشد. به این حالت نرمال بودن چندگانه می گویند. شکل
زیر نرمال بودن دو متغیر را به صورت هم زمان نشان می دهد.

مفهوم واریانس و انحراف معیار