مشتقات جزئی
مقدمه
مشتقهای جزئی وقتی به دست می آیند که در یک تابع چند متغیره همه
متغیرها را به جز یکی ثابت نگه داریم و نسبت به آن متغیر مشتق بگیریم.
تعریف
اگر (x0 , y0) نقطه ای از دامنه یک تابع مثل z=f(x,y) باشد، محل تقاطع
صفحه y=y0 با رویه z=f(x,y) خم z=f(x0,y0) است. این خم نمودار تابع
z=f(x,y0) در صفحه y=y0 است. در این صفحه مختص قائم z است و آن فاصله نقطه
واقع در بالای (پایین) صفحه xy از این صفحه است. مختص افقی x است. مشتق
z=f(x, y0) نسبت به x در x=x0 طبق معمول تعریف می شود و عبارت است از حد
فرمول*****
به شرطی که این حد موجود باشد. این حد را مشتق جزئی f نسبت به x در
نقطه (x0,y0) می نامیم. شیب خم ذکر شده در صفحه y=y0 در نقطه
(x0,y0,f(x0,y0)) مقدار این مشتق جزئی نسبت به x در (x0,y0) است. مماس بر
خم در x=x0 خطی واقع در صفحه y=y0 است که از نقطه (x0,y0,f(x0,y0)) می گذرد
و شیب آن این مقدار است.
نمادهای معمول مشتق جزئی z=f(x,y) نسبت به x در (x0,y0):
یا که مشتق جزئی f نسبت به x در (x0,y0) یا f اندیس x در (x0,y0) است. این نماد برای تاکید بر نقطه (x0,y0) مناسب است.
- : مشتق جزئی z نسبت به x در نقطه (x0,y0) است. این نماد در
علوم مهندسی به کار می رود که با متغیرها سروکار داشته باشیم و تابع به طور
صریح ذکر نشود. - یا : مشتق جزئی f (یا z) نسبت به x است. این نماد وقتی مناسب است که مشتق جزئی ، خود به عنوان یک تابع در نظر گرفته شود.
تعریف مشتقات جزئی توابع با بیش از دو متغیر مستقل ، شبیه تعریف
مربوط به توابع دومتغیره است. این مشتقات همان مشتق های معمولی نسبت به یک
متغیرند با این شرط که سایر متغیرهای مستقل ، ثابت درنظر گرفته شوند.
مشتقات جزئی با متغیرها ی مقید:
هنگام محاسبه مشتقات جزئی توابعی نظیر w=f(x,y) تاکنون فرض کردیم که
y,x مستقل اند. ام در بسیاری از موارد کاربردی این وضع برقرار نیست. مثلا
انرژی درونی (U) یک گاز را می توان برحسب فشار ، P ، حجم ، V ، و دما ، T ،
بیان کرد.
U=f(P,V,T)
اما اگر این گاز ایده آل باشد از اطلاعات فیزیکی خود می دانیم که در
این صورت T , V , P از قانون گازهای ایده آل یعنی PV=nRT (R,n ثابت)
تبعیت می کنند و لذا مستقل نیستند. محاسبه مشتقات جزئی در این گونه
موارد ممکن است پیچیده باشد. این گونه موارد در اقتصاد ، مهندسی یا فیزیکی
بوفور یافت می شود.
اگر متغیرهای z,y,x تابعی چون w=f(x,y,z) با رابطه ای مانند معادله
z=x2+y2 مقید شوند . تعبیر هندسی و مقادیر عددی مشتقات جزئی f بستگی به این
خواهند داشت که چه متغیرهایی را وابسته و چه متغیرهایی را مستقل انتخاب
کنیم. این انتخاب اثر فوق العاده ای بر نتیجه می گذارد. این تاثیر نه تنها
در مقدار عددی مشتق جزئی نمودار می شود بلکه شکل هندسی تابع نیز از این
انتخاب متاثر می گردد.
مشتق های جزئی مراتب بالاتر ، معادلات دیفرانسیل جزئی مربوط به فیزیک:
اگر از تابعی مکررا مشتق جزئی بگیریم، مشتق هایی به دست می آیند که
مشتق های مراتب بالاتر (یعنی بالاتر از مرتبه اول) نام دارند. این مشتق ها
در معادلاتی ظاهر می شوند که قوانین فیزیکی مهمی را در مورد حرکت موج ،
جریان گرما و گرانش بیان می کنند. این مشتقات در آزمون های مربوط به مشخص
کردن ماکسیمم ها و مینیمم های توابع با بیش از یک متغیر ظاهر می شوند.
معمولا حل معادلات دیفرانسیلی که شامل مشتق های جزئی اند دشوار است.
بخشی از این دشواری بدلیل گوناگونی جواب است. وقتی از تابعی چون f(x,y)
دوبار کشتق می گیریم مشتق های مرتبه دوم آن را بدست می آوریم. این مشتقات
را معمولا با نماد زیر نمایش می دهیم.
فرمول****
دو نماد اول از سمت راست ، با یکدیگر برابرند و این یک امر اتفاقی
نیست. زیرا در هر نقطه ای که f ، fx ، fy ، fxy و fyx پیوسته باشند مشتقات
جزئی آمیخته fxy و fyx باید با هم برابر باشند این واقعیت را قضیه مشتقهای
آمیخته می نامیم.
معادله یک بعدی گرما (=معادله پخش=معادله تلگراف)
فرض کنیم w(x,t) دمای نقطه x از میله رسانای یکنواختی در لحظه t باشد و
جریان گرما از دیواره لوله به هیچ وجه عبور نمی کند در این صورت ، مشتق
های جزئی wxx و wt در یک معادله دیفرانسیل به صورت زیر صدق می کنند.
این معادله را معادله یک بعدی گرما می نامند. مقدار C2 از روی جنس میله
تعیین می شود. این معادله در بدست آوردن دمای فصلی زیر سطح زمین کارساز
است. در شیمی و زیست شناسی گرما را معادله پخش می نامند. در مهندسی برق
معادله گرما به معادله تلگراف معروف است و به صورت های Vxx=RCVt و ixx=RCit
ظاهر می شود. این معادلات ولتاژ V و جریان I را در یک کابل هم محور یا در
هر کابل دیگری توصیف می کنند که در آنها نشت و القا کنایی قابل اغماض اند.
معادلات لاپلاس
در معادله لاپلاس سه بعدی توزیع های دمای حالت پایا که در آن T تابعی
است از f برحسب دو متغیر z,y,x . در فضا ، پتانسیل های گرانشی و پتانسیل
های الکترواستاتیکی صدق می کند و عبارت است از اینکه مجموع مشتقات مرتبه
دوم f نسبت به هر یک از متغیرهای z,y,x برابر صفر است. معادله لاپلاس در
فضای دو بعدی نیز برقرار می باشد.
معادله موج: اگر در ساحل اقیانوسی بایستیم و در لحظه ای از زمان از
امواج عکس بگیریم آنگاه در عکس الگوهای منظمی از برآمدگی ها و فرورفتگی ها
نمایان خواهد بود. در فضا حرکت قائم متناوب نسبت به فاصله را می بینیم. اگر
روی آب باشیم با عبور امواج می توانیم بالا و پایین رفتن آب را حس کنیم.
در فیزیک ، این تقارن زیبا را با معادله یک بعدی موج یعنی
بیان می کنند که در آن w ارتفاع موج ، x متغیر فاصله ، t متغیر زمان و C سرعت انتشار موج است.
کاربردها: بخشی از کاربردها در بالا توضیح داده شد ولی برای آشنایی بیشتر به مقاله کاربردهای مشتقات جزئی مراجعه فرمایید.
مشتق
مشتق یکی از مهمترین مفاهیم ریاضی است. بوسیله مشتق میتوان برخی از مفاهیم فیزیکی (مانند سرعت و شتاب)با تعاریف ریاضی بیان نمود.
ااگر منحنی یک تابع را در فضای دو بعدی در نظر بگیریم بوسیله مشتق میتوانیم شیب خط مماس بر منحنی را در هر نقطه دلخواه بدست آوریم.همچنین با استفاده از مشتق میتوان خواص هندسی منحنی یک تابع مانند تقعر و تحدب را مشخص کرد.
البته باید به این نکته توجه کرد که هر تابعی در هر نقطه نمیتواند مشتق
داشته باشد و به طور کلی مشتق پذیری یک تابع در یک نقطه شرایط خاصی
میطلبد.
مشتق گیری و مشتق پذیری
در گذشته های نه چندان دور، مشتق یک تابع را به صورت زیر نشان می دادند:
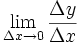
که در این فرمول نشان دهنده میزان تغییرات یک کمیت است. ولی در حال حاضر برای محاسبه مشتق توابع،بیشتر از فرمول زیر استفاده میکنند:
نشان دهنده میزان تغییرات یک کمیت است. ولی در حال حاضر برای محاسبه مشتق توابع،بیشتر از فرمول زیر استفاده میکنند:
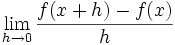
معمولا از نمادهای زیر برای نشان دادن مشتق تابع f نسبت به متغیر x، استفاده میکنند:
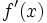 |
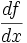 |
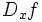 |
یک تابع را در نقطه ای مانند x مشتق پذیر گویند اگردر آن نقطه مشتق
موجود باشد. و برای مشتق پذیری تابع در یک بازه لازم است تابع در هر نقطه
دلخواه از بازه مشتق پذیر باشد.اگر تابع در نقطه ای مانند c پیوسته
نباشد آنگاه در c نمیتواند مشتق پذیر باشد.البته لازم به ذکر است که
پیوستگی در یک نقطه وجود مشتق را تضمین نمیکند.مشتق یک تابع مشتق پذیر
میتواند خود نیز مشتق پذیر باشد،که به مشتق آن مشتق دوم تابع گویند.مشتق
مراتب بالاتر نیز به همین ترتیب تعریف میشوند.
بررسی مشتق از نظر هندسی
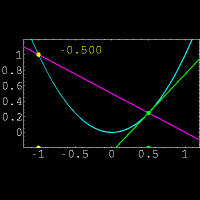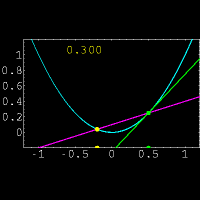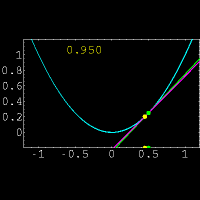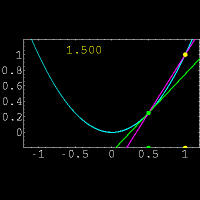 |
از نظر هندسی مشتق یک تابع در یک نقطه دلخواه ،شیب خط مماس بر منحنی در
آن نقطه است.البته پیدا کردن مستقیم شیب خط مماس در یک نقطه کار دشواری
است.زیرا فقط مختصات یک نقطه از خط مماس را داریم.(برای پیدا کردن شیب یک
خط از مختصات دو نقطه بر روی خط استفاده میکنیم)برای حل این مشکل از یک خط
متقاطع استفاده کرده و این خط را به خط مماس نزدیک میکنیم.برای درک بهتر
موضوع به شکل مقابل توجه نمایید.در این شکل خط متقاطع با رنگ بنفش و خط
مماس با رنگ سبز مشخص شده است و عددی که در تصویر تغییر میکند نشان دهنده
شیب خط متقاطع میباشد. حال از دیدگاه ریاضی این روش را بیان میکنیم:
از دیدگاه ریاضی بدست آوردن مشتق با حدگیری
از شیب خط قاطع که به خط مماس نزدیک شده است بدست می آید.پیدا کردن شیب
نزدیکترین خط متقاطع به خط مماس با استفاده از کوچکترین h در فرمول زیر
حاصل میشود:
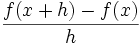
| عکس پیدا نشد |
|
در این فرمول h به عنوان کوچکترین تغییر متغیر x تعریف میشودو میتواند
مقدار مثبت یا منفی اختیار کند. در این فرمول شیب خط با استفاده از نقاط 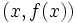 و
و 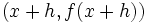
حاصل میشود.واضح است که در این روش فقط یک نقطه روی خط برای ما معلوم است
و نیازی برای بدست آوردن نقطه دوم روی خط وجود ندارد.همچنین در این روش
مشتق x ،حاصل حد زیر است:
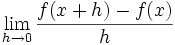
ارتباط مشتق با علم فیزیک
مشتق نقش مهمی در تعریف برخی ار کمیتهای فیزیک حرکت دارد.ما با داشتن موقعیت اجسام بر حسب زمان میتوانیم سرعت و شتاب
آنها را محاسبه کنیم.اگر ما از معادله مکان جسم بر حسب زمان مشتق بگیریم
معادله سرعت بدست میآید و اگر از معادله سرعت مشتق گیری نماییم(مشتق دوم
معادله مکان)معادله شتاب حاصل میشود.
نقاط بحرانی
نقاطی از تابع که به ازای آنها مشتق تابع تعریف نشده و یا برابر
صفر باشد را نقاط بحرانی مینامند.اگر مشتق دوم در یک نقطه بحرانی مثبت
باشد،آن نقطه مینیمم نسبی است.و اگر منفی باشدماکزیمم نسبی است،و اگر برابر
صفر باشد ممکن است ماکزیمم و مینیمم نسبی نباشد.مشتق گرفتن و بدست آوردن
نقاط بحرانی،اغلب ساده ترین راه برای پیدا کردن مینیمم و ماکزیمم نسبی
است.(در بهینه سازی نیز این روش بسیار مفید است.به طور کلی مینیمم و ماکزیمم نسبی فقط میتوانند جزئ نقاط بحرانی باشند.
تجزیه و تحلیل نمودارها
مشتق ابزار مناسبی برای آزمودن نمودار تابع است. نقاطی از دامنه تابع که به ازای آنها مشتق اول برابر صفر شود میتوانند نقاط اکسترمم نسبی تابع باشند.البته باید توجه کرد که تمام نقاط بحرانی نقاط اکسترمم نسبی نیستند.برای مثال تابع 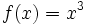 یک نقطه بحرانی در x=0 دارد، ولی میتوان از نمودار تابع متوجه این نکته شد که تابع در این نقطه دارای ماکزیمم یا مینیمم نسبی نیست.
یک نقطه بحرانی در x=0 دارد، ولی میتوان از نمودار تابع متوجه این نکته شد که تابع در این نقطه دارای ماکزیمم یا مینیمم نسبی نیست.
آزمون مشتق اول و آزمون مشتق دوم
، روش هایی را برای تشخیص نقاط ماکزیمم و مینیمم نسبی فراهم میکند.لازم به
ذکر است در فضاهای چند بعدی نقاط اکسترمم را با استفاده از مشتقات جزئی بدست میآورند.



