مشتق بزبان ساده

عمل دوتایی

آشنایی

شاید تابه حال فرایندهای زیادی را دیده باشید که طی آن دو چیز با هم ترکیب می‌شوند و شی سوم متمایزی را حاصل می دهند.

مثلاً تصور کنید در یک کلاس درس معلم کلاس می‌گوید “ب”، “آ” و دانش
آموزان باهم فریاد می‌زنند “با”. این بار معلم می‌گوید “ب”، “و” و اینبار
دانش‌آموزان فریاد می‌زنند “بو” و یا در مثالی دیگر در طبیعت ملکول‌های
هیدروژن و اکسیژن با هم ترکیب شده و ماده سومی چون آب را پدید می‌آورد.

این ها همگی نمونه‌هایی از اعمالی دوتایی هستند که در طی آنها دو عنصر شرکت کننده عنصر سومی را پدید می‌آورند.

اعمال دوتایی و به دنبال آن ساختارهای جبری از مهم‌ترین و مقدماتی‌ترین مفاهیم در جبر مجرد هستند. در ادامه به تعریف دقیق یک عمل دوتایی در جبر می‌پردازیم و ویژگی‌های آنها را بررسی می‌کنیم.

عمل دوتایی

یک عمل دوتایی روی مجموعه ناتهی G تابعی است چون 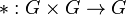$*: G \times G \to G$ از G×G به توی G که به هر عضو (a,b) از G×G یک عضو یکتا چون C از G را نسبت می‌دهد.

لازم به یادآوری است که G×G حاصل ضرب دکارتی G در خودش است.

با توجه به تعریف یک عمل دوتایی، یک عمل دوتایی چون * روی یک مجموعه ناتهی G باید واجد شرایط زیرباشد:

عمل دوتایی روی کل دامنه خود یعنی G×G تعریف شده باشد.
عمل دوتایی * یک تابع خوش‌ تعریف از G×G به توی G باشد یعنی به هر عضو G×G عنصر یکتایی از G را نسبت می‌دهد.
حاصل ترکیب دو عضو (a,b) تحت یک عمل دوتایی باید متعلق به G باشد. به عبارت دیگر مجموعه G نسبت به عمل دوتایی خود بسته باشد.
عمل دوتایی را که سبب ترکیب هر دو عضو مجموعه ناتهی G می‌شود، معمولاً با * یا ° نمایش میدهیم.

برای نمایش اینکه، * یک عمل دوتایی تعریف شده در مجموعه ناتهی G باشد می‌نویسم (*,G) و برای هر (a,b) عضو G×G، حاصل عمل * روی زوج مرتب (a,b) را به صورت (a,b)* یا معمول‌تر به فرم a*b نشان می دهیم و معمولاً برای سهولت در نوشتن a*b را نیز به صورت ab می‌نویسیم.

همچنین معمولاً یک عمل دوتایی روی یک مجموعه‌ را با دو نماد جمعی + و
ضربی . نشان می‌دهیم که نباید آنها را با جمع و ضرب اعداد خلط کرد.

اگر عمل دوتایی را به فرم جمعی نشان دهیم حاصل عمل + را روی (a,b) به
صورت a+b نشان می‌دهیم و اگر عمل عمل را با نماد ضربی نشان دهیم حاصل عمل
را به صورت a.b یا ab نشان می‌دهیم.

مثال هایی از اعمال دوتایی

مجموعه اعداد صحیح را در نظر بگیرید، عمل * را روی 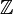$\mathbb{Z}$ را به صورت زیر تعریف می‌کنیم:

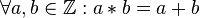
$\forall a,b \in \mathbb{Z} : a*b = a+b$

که همان عمل جمع اعداد صحیح است و به آسانی دیده می‌شود * یک عمل دوتایی است.

مجموعه اعداد طبیعی را در نظر بگیرید. * با ضابطه زیر ، یک عمل دوتایی است:

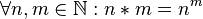
$\forall n,m \in \mathbb{N} : n*m= n^m$

اما عمل فوق در اعداد صحیح و اعداد گویا عمل دوتایی نمی‌باشد. زیرا به عنوان مثال

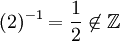
$(2)^{-1}=\frac{1}{2}\not \in \mathbb{Z}$

یا

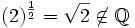
$(2)^{\frac{1}{2}}=\sqrt{2}\not \in \mathbb{Q}$

ولی در مجموعه اعداد حقیقی عمل فوق ، یک عمل دوتایی است.

عمل * را در مجموعه دلخواه A به صورت زیر تعریف می‌کنیم:

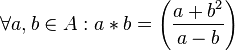
$\forall a,b \in A : a*b = \left ( \frac{a+ b^2 }{a-b} \right )$

عمل * در مجموعه اعداد گویا یک عمل دوتایی نیست . چرا که به ازای a=b جواب a*b تعریف نشده می‌شود.

بسته بودن نسبت به یک عمل

مجموعه اعداد صحیح و عمل جمع اعداد را در نظر بگیرید. عمل جمع اعداد یک
عمل دوتایی روی مجموعه اعداد صحیح است و بدیهی است که با توجه به تعریف عمل
دوتایی روی 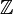$\mathbb{Z}$ برای هر دو عدد صحیح a و b عدد a+b نیز عددی صحیح است.

حال مجموعه اعداد صحیح زوج 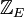$\mathbb{Z}_E$ که زیرمجموعه‌ای از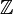 $\mathbb{Z}$
است را در نظر بگیرید. برای هر دو عضو این مجموعه چون m و n چون مجموع دو
عدد زوج، عددی زوج است عدد m+n زوج است پس متعلق به مجموعه اعداد صحیح زوج
است.

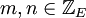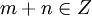
به عبارت برای هر $m,n\in \mathbb{Z}_E$ داریم $m+n\in Z$

در این حالت اصطلاحاً می‌گوییم مجموعه اعداد صحیح زوج تحت عمل جمع بسته است.

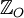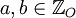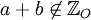اما همواره برای هر زیرمجموعه Z چنین نیست. مثلاً مجموعه اعداد صحیح فرد $\mathbb{Z}_O$ را در نظر بگیرید. مجموع دو عدد صحیح فرد عددی زوج است که دیگر به مجموعه اعداد صحیح فرد تعلق ندارد پس برای هر $a,b\in \mathbb{Z}_O$ داریم $a+b\not \in \mathbb{Z}_O$ در این حالت می‌گوییم مجموعه اعداد صحیح فرد تحت عمل جمع بسته نمی‌باشد.

اگر G یک مجموعه ناتهی و * یک عمل دوتایی تعریف شده روی G باشد و E
زیرمجموعه ای ناتهی از G باشد، می گوییم E تحت عمل G بسته است در صورتیکه
به ازای هر a,b∈E داشته باشیم a*b∈E.

به عنوان مثال:

ویژگی‌های اعمال دوتایی

یک عمل دوتایی روی یک مجموعه می تواند دارای برخی ویژگی‌های خاص باشد.

شرکت پذیری

فرض کنید * یک عمل دوتایی روی مجموعه ناتهی G باشد. در این صورت
می‌گوییم عمل * روی G شرکت پذیر است هرگاه برای هر a,b,c متعلق به مجموعه G
داشته باشیم: a*(b*c)=(a*b)*c

به عنوان مثال:

در مجموعه اعداد صحیح عمل * را به صورت زیر بیان میکنیم:

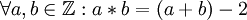
$\forall a,b \in \mathbb{Z} : a*b= (a+b)-2$

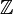$\mathbb{Z}$ تحت عمل * شرکت پذیر است.

روی مجموعه اعداد صحیح عمل * را به صورت زیر بیان میکنیم :

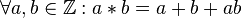
$\forall a,b \in \mathbb{Z} : a*b= a+b+ab$

عمل * روی 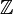$\mathbb{Z}$ خاصیت شرکت پذیری دارد.

عمل تفاضل در مجموعه اعداد حقیقی خاصیت شرکت پذیری ندارد.

نیم‌گروه

مجموعه (*,G) یک نیم‌گروه
است هر گاه عمل * روی G شرکت پذیر باشد. به عنوان مثال مجموعه اعداد طبیعی
به همراه عمل جمع یک نیم گروه است ولی مجوعه اعداد صحیح به همراه عمل
تفاضل یک نیم گروه نمی باشد.

هرگاه 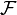$\mathcal{F}$ مجموعه توابع پیوسته به روی اعداد حقیقی باشد ، آنگاه 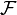$\mathcal{F}$ تحت عمل جمع توابع ، یک نیم‌گروه است.
مجموعه توابع تعریف شده روی اعداد حقیقی تحت عمل ترکیب توابع ، یک نیم‌گروه است.

جابجایی

فرض کنید G مجموعه‌ای ناتهی و * یک عمل دوتایی روی G باشد. در این صورت
عمل * را روی G جابجایی می‌گوییم هر‌گاه برای هر دو عضو a و b متعلق به
مجموعه G داشته باشیم a*b=b*a.

به عنوان مثال عمل جمع اعداد روی اعداد طبیعی عملی جابجایی است و عمل تفریق روی مجموعه اعداد حقیقی دارای خاصیت جاجایی نمی‌باشد.

عضو خنثی

فرض کنید G مجموعه‌ای ناتهی و * یک عمل دوتایی تعریف در G باشد. در این صورت عضو e متعلق مجموعه G را عضو خنثی یا همانی G نسبت به عمل * می‌گوییم هرگاه برای هر a متعلق به مجموعه G داشته باشیم: e*a=a*e=a

اگر e عضو G چنان باشد که برای هر a عضو G داشته باشیم a*e=a آنگاه e را
عضو خنثی راست می‌گوییم و اگر برای هر a متعلق به G داشته باشیم
e*a=aآنگاه e را عضو خنثی چپ می‌گوییم.

به عناون مثال در مجموعه اعداد صحیح به همراه عمل جمع عدد صحیح صفر عضو خنثی عمل جمع است و عضو خنثی ضرب در مجموعه ماتریس‌های مربعی از مرتبه n ماتریس همانی است.

حال ممکن است این سوال پیش بیاید که آیا یک مجموعه نسبت به یک عمل
دوتایی می‌تواند دارای دو عضو خنثی باشد؟ قضیه زیر بیان می کند عضو خنثی یک
ساختمان جبری در صورت وجود یکتاست.

قضیه
عضو خنثی یک ساختمان جبری در صورت وجود منحصر بفرد است.
برهان
فرض کنید (*,G) یک ساختمان جبری با دو عضو خنثی e1 و e2 باشد. نشان میدهیم e1=e2

چون e2∈G و e1 عضو خنثی G نسبت به عمل * است داریم

e1 * e2 = e2

و چون e1∈G و e2 عضو خنثی G است داریم:

e1 * e2 = e1

که دو تساوی اخیر نشان می دهد e1=e2 و حکم ثابت می شود.

عضو معکوس

فرض کنید G یک مجموعه ناتهی و * یک عمل دوتایی روی G باشد و e عضو خنثی G
نسبت به عمل * باشد. در این صورت عضو a متعلق به G را نسبت به عمل * وارون
پذیر (معکوس پذیر) می‌نامیم هرگاه عضوی چون b موجود باشد که a*b=b*a=e.

همچنین اگر b چنان موجود باشد که a*b=e گوییم b معکوس راست a است و اگر bچنان باشد که b*a=e آنگاه b را معکوس چپ a مِی‌نامیم

آموزش و پرورش از دیدگاه بزرگان

ملت از راه آزادی به تعلیم و تربیت دست می یابند، نه برعکس.((جرج برنارد شاو))

قبل از ازدواج شش نظریه درباره تربیت کودکان داشتم؛ حالا شش فرزند دارم، ولی دارای هیچ گونه نظریه ای نیستم.((لورد روچستر))

بزرگترین کارخانه نابودی توانمندیها ، آیین آموزشی نادرست است.((حکیم ارد بزرگ))

مردی
را که آماده آموختن است تعلیم ندادن، انسانی را به هدر دادن است، مردی را
که آماده آموختن نیست تعلیم دادن، سخن به هدر دادن است، خردمند نه انسان را
به هدر می دهد و نه سخن را.((کنفوسیوس))

می توان در ظرف دو سال یک
کارخانه ذوب آهن ساخت، ولی برای تربیت یک مدیر برای این صنعت باید بیست سال
وقت صرف کرد. ((جواهر لعل نهرو ))

مهد پرورش خرد، آغوش عقل نیست،
بلکه دامان عشق است. نهال خرد باید در کوزه عشق کاشته شود و با آب احساسات
آبیاری گردد.((موریس مترلینگ))

از کسی که نمی داند که نمی داند،
دوری کن، به کسی که نمی داند و می داند که نمی اند، تعلیم بده، کسی را که
می داند و نمی داند که می داند، روشن کن و از کسی که می داند و می داند که
می داند پیروی کن.((مثل تازی))

هرگز به کودک تان نگویید پیشه آینده
اش چه باشد. همواره به او ادب و ستایش به دیگران را آموزش دهید، چون با
داشتن این ویژگیها همیشه او نگار مردم و شما در نیکبختی خواهید بود و اگر
این گونه نباشد، هیچ پیشه ای نمی تواند به او و شما بزرگواری بخشد.((حکیم
ارد بزرگ))

مشکلات ما را متوقف نمی کنند، بلکه به ما آموزش می دهند.((برایان تریسی))

آموزش احمقها به همان اندازه بی نتیجه است که بخواهیم با صابون، ذغال را سفید کنیم.((کیتز))

دریای بی تلاطم، هیچگاه دریانورد ورزیده تربیت نمی کند.((مثل آفریقایی))

ما چیزهایی را آموزش می دهیم که می دانیم، ما مانند خودمان را بازسازی می کنیم. گندم از گندم بروید، جو ز جو.((جان ماکسول))

معنای حیات دنیوی، بر خلاف آنچه به ما آموخته اند، در رفاه و رونق و آسایش تن نیست، در پرورش جان است.((الکساندر سولژنیستن))

رهبران
حقیقی کسب و کار، جوامع حرفه ای، تعلیم و تربیت و حکومت و خانه، در مقایسه
با دیگر افراد جامعه برتریهایی دارند که آنها را از دیگران متمایز می کند.
برتری آنها در ولادت استثنایی، هوشبهر بالا یا در استعداد خاص نیست. برتری
آنها در دیدگاه و نگرش آنها است نه در شایستگی و استعداد آنها.((دنیس
ویتلی))

وقتی خدا می خواهد کسی را تربیت کند او را به مدرسه های پر
زرق و برق نمی فرستد، بلکه او را در مدرسه احتیاج تعلیم می دهد.((جان
ماکسول))

مدتهاست به این امر پی برده ام که آموزش دادن یک کار خوب
به بیست نفر راحت تر از این است که خودم یکی از آن بیست نفر باشم که می
بایست به دستورات خودم عمل کنم.((دیل کارنگی))

هیچ وقت نباید کسی را
به دلیل عملش تحقیر و یا به جهت کاری که کرده توبیخ کنیم. چون او در محیطی
رشد کرده که مقتضیات تربیتی و محیط و عادتهای اکتسابی و ارثی خود را داشته
است.((آبراهام لینکلن))

چرا از فرزندانی که خود آنها را قدر ناشناس پرورش داده و تربیت کرده ایم، گله مندیم؟((دیل کارنگی))

بهترین شیوه آموزش به کودک ، همراه شدن با او در درون داستانهای پند آموز است.((حکیم ارد بزرگ))

فرزندان ما همان گونه می شوند که تربیت شده اند.((دیل کارنگی))

مشتق بزبان ساده